
Introduction
IMU Overview
IMUs (Inertial Measurement Units) are remarkable sensors that measure the movement and orientation of the devices they are embedded in. Since the rise of smartphones, their size and cost have been drastically reduced, enabling a wide range of applications in robotics and drones, where they enable autonomous navigation and guidance.
IMUs combine a gyroscope (measuring angular velocity in °/s or rad/s) and an accelerometer (measuring linear acceleration in m/s² or g). Gyroscopes measure rotation but can drift over time, while accelerometers sense velocity changes and tilt but cannot distinguish between motion and gravity. Sensor fusion algorithms correct gyroscope drift with accelerometer data and stabilize accelerometer noise with gyroscope input, ensuring accurate motion tracking.
At the heart of an IMU is a Micro-Electro-Mechanical System (MEMS): a tiny structure, often just a few microns in size (about 1/100th the width of a human hair), that moves slightly in response to forces. These movements generate changes in voltage, which are measured by the sensor, converted into numerical data, and transmitted to your system through communication protocols such as SPI or I²C.

Micro-scale mechanical elements within a MEMS-based Inertial Measurement Unit (IMU).
For everyday devices like smartphones or tablets, precision isn't as important, so IMUs are not necessary factory-calibrated for temperature. But for drones and robots used in outdoor conditions, accuracy matters and calibrating the IMU for temperature can greatly improve its performance.
Calibration Purpose
Thermal calibration involves placing the IMU-equipped Printed Circuit Board Assembly (PCBA) in a climate chamber for several hours while varying the temperature. With the IMU kept flat and motionless, any changes in its measurements are attributed to temperature effects. The resulting data is used to calculate and save calibration parameters specific to each board. During operation, these parameters are applied in real time to compensate for temperature-induced measurement variations.
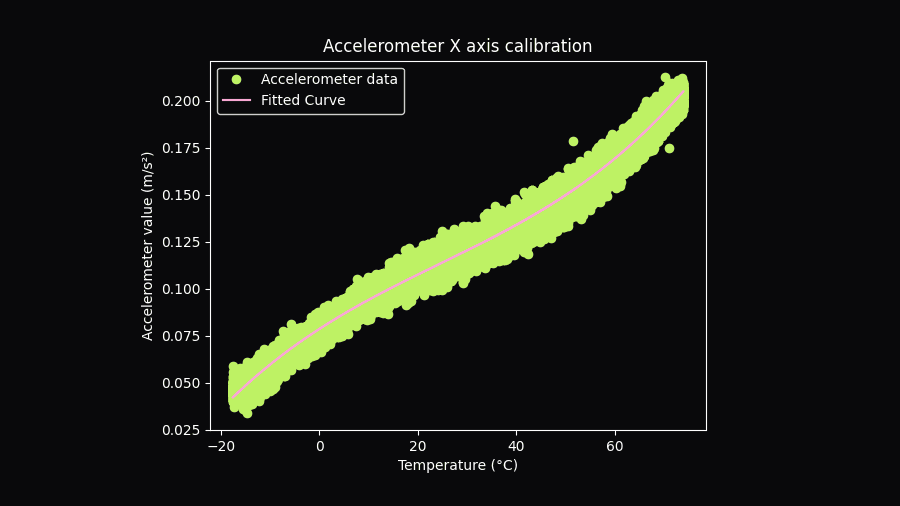
Curve showing accelerometer X vs. temperature with a polynomial fit for calibration.
Most Electronic Manufacturing Service (EMS) providers have climate chambers for tasks like stress testing, so reserving one for your boards shouldn't be an issue. For lab use, you can purchase a small climate chamber for under $5,000, suitable for testing a few boards. The cost largely depends on the chamber's temperature range. For instance, testing a drone designed for outdoor use may require a chamber that operates between -20°C and 70°C to simulate extreme environmental conditions.
Note that the temperature measured by the IMU will always be higher than the chamber's temperature due to the internal heat generated by the IMU's casing and the PCBA it is mounted on.
Equipment & Setup
To implement thermal calibration for the IMU in a drone, you will need the following:
- A climate chamber capable of reaching temperatures between -20°C and 70°C.
- A support structure to hold the PCBA in the chamber and a power supply.
- A Device Under Test (DUT), equipped with the IMU that requires calibration.
- Firmware for the device, with a triggerable mode to log the raw IMU data.
- A Python test script, built with OpenHTF, to:
- Retrieve data from each board after the calibration process.
- Calculate the calibration parameters.
- Verify the quality of the calibration and ensure there are no defects.
- Save the calibration parameters to the product.
- A database and analytics platform, like TofuPilot, which will store these calibration data for traceability and monitoring purposes.
Hardware Components
Climate Chamber
We will use the Votsch VT4002 temperature test chamber, which has a temperature range of -40°C to +130°C. With its 16-liter volume, it is ideal for designing the test in the lab or for small production runs.

The Votsch VT4002 is a compact lab test chamber with a -40°C to +130°C range.
Cycle Program
The IMU's response is not necessarily the same when it heats up versus when it cools down. To ensure the calibration accurately reflects the sensor's real thermal behavior, we will set a calibration duration of 2 hours, with 4 temperature cycles ranging from -20°C to 70°C.
Support Structure
For the lab setup, we'll create a simple 3D-printed support using ESD filament. Foam will be added to reduce vibrations from the climate chamber. While these vibrations are likely filtered out during data processing, minimising them is still beneficial.
In mass production, we can collaborate with the test team at our EMS to design a support that accommodates multiple boards to optimise throughput, provides power to them, and is adapted to the dimensions of their temperature test chambers.
Custom Firmware
Throughout the entire calibration process, the IMU needs to log its measurements at a frequency of at least 10 Hz. To enable this, we will develop a special logging mode in the firmware. When activated, this mode will start data acquisition and record the following parameters:
- Timestamp: To track when each measurement was taken.
- Gyroscope data: X, Y, and Z axes in degrees per second (deg/s).
- Accelerometer data: X, Y, and Z axes in meters per second squared (m/s²).
- Internal sensor temperature: This will be used as the reference for calibration.
The logged data can be stored as a JSON or CSV file in the PCBA memory or on an SD card. Most climate chambers have an external pin that activates at program start. Connecting this pin to a stabilized power supply outside the chamber allows the supply to switch on automatically at the program's start and off at its end, ensuring logging occurs only during the thermal cycle and not afterward, such as when the operator retrieves the board.
Test Script
Overview
Once the thermal cycle is complete, the chamber powers off and the log file is ready for retrieval and processing. Operators will remove the PCBAs from their calibration support and connect them to the test station. At this point, the script takes over to:
- Connect to the Device Under Test (DUT) and retrieve the acquisition file.
- Validate the acquired data.
- Process the calibration data.
- Validate the calibration parameters.
- Save calibration results to the DUT internal memory.
- Provide a global pass/fail status.
- Log results to the test database TofuPilot for traceability and analytics.
Execution Framework
For our test script development, Python is a great choice because it's simple, fast to develop with, and comes with powerful libraries for data analysis and visualization.
On top of Python, we'll use the OpenHTF library to manage multiple test phases, log numeric measurements and attachments, and provide a repeatable way to write tests and record results.
Main Script
Using OpenHTF, we define a test script with two phases: one to retrieve the acquisition file from the DUT and apply validation measurements on the raw data, and another to compute thermal calibration parameters and apply validation measurements on the calibration output.
Utility functions are separated in a dedicated utils folder, and interactions with external devices, like the DUT, are handled through plugs, which are automatically destroyed at the end of the test by their tearDown method.
import openhtf as htf
from openhtf import Test, measures
from openhtf.plugs import plug
from openhtf.util import units
from plugs.mock_dut import MockDutPlug
from tofupilot.openhtf import TofuPilot
from utils.calibrate_sensor import calibrate_sensor
from utils.compute_noise_density import compute_noise_density
from utils.compute_r2 import compute_r2
from utils.compute_residuals import compute_residuals
from utils.compute_temp_sensitivity import compute_temp_sensitivity
@plug(dut=MockDutPlug)
def connect_dut(test: Test, dut: MockDutPlug) -> None:
"""Connect to the Device Under Test (DUT)."""
dut.connect()
@measures(
*(
htf.Measurement("{sensor}_noise_density_{axis}")
.doc("Noise density, normalized to √Hz")
.in_range(0.0, {"acc": 0.003, "gyro": 0.005}.get(sensor))
.with_units(
{
"acc": units.METRE_PER_SECOND_SQUARED,
"gyro": units.DEGREE_PER_SECOND,
}.get(sensor)
)
.with_args(sensor=sensor, axis=axis)
for sensor in ("acc", "gyro")
for axis in ("x", "y", "z")
),
*(
htf.Measurement("{sensor}_temp_sensitivity_max_{axis}")
.doc("Max temperature sensitivity (unit/°C)")
.with_units(
{
"acc": units.METRE_PER_SECOND_SQUARED,
"gyro": units.DEGREE_PER_SECOND,
}.get(sensor)
)
.with_args(sensor=sensor, axis=axis)
for sensor in ("acc", "gyro")
for axis in ("x", "y", "z")
),
*(
htf.Measurement("{sensor}_temp_sensitivity_ref_{axis}")
.doc("Temperature sensitivity at 25°C (unit/°C)")
.in_range(
{
"acc": {"x": 5e-4, "y": 5e-4, "z": 5e-4},
"gyro": {"x": 6e-5, "y": 6e-5, "z": 6e-5},
}[sensor][axis],
{
"acc": {"x": 1e-2, "y": 1e-2, "z": 1e-2},
"gyro": {"x": 1e0, "y": 1e0, "z": 1e0},
}[sensor][axis],
)
.with_units(
{
"acc": units.METRE_PER_SECOND_SQUARED,
"gyro": units.DEGREE_PER_SECOND,
}.get(sensor)
)
.with_args(sensor=sensor, axis=axis)
for sensor in ("acc", "gyro")
for axis in ("x", "y", "z")
),
)
@plug(dut=MockDutPlug)
def get_calibration_data(test: Test, dut: MockDutPlug) -> None:
"""Retrieve calibration data from the DUT."""
test.state.update(dut.get_imu_data(test))
for sensor, data_key in [("acc", "acc_data"), ("gyro", "gyro_data")]:
sensor_data = test.state[data_key]
temperature = sensor_data["temperature"]
axes_data = {axis: sensor_data[f"{sensor}_{axis}"]
for axis in ["x", "y", "z"]}
for axis, axis_data in axes_data.items():
noise_density = compute_noise_density(axis_data)
temp_sensitivity = compute_temp_sensitivity(axis_data, temperature)
test.measurements[f"{sensor}_noise_density_{axis}"] = noise_density
test.measurements[f"{sensor}_temp_sensitivity_max_{axis}"] = (
temp_sensitivity["max_sensitivity"]
)
test.measurements[f"{sensor}_temp_sensitivity_ref_{axis}"] = (
temp_sensitivity["sensitivity_at_ref"]
)
@measures(
*(
htf.Measurement("{sensor}_polynomial_coefficients_{axis}")
.doc("Calibration polynomial coefficient matrix")
.with_args(sensor=sensor, axis=axis)
for sensor in ("acc", "gyro")
for axis in ("x", "y", "z")
),
*(
htf.Measurement("{sensor}_residual_mean_{axis}")
.doc("Residual mean")
.in_range(0.0, {"acc": 0.01, "gyro": 0.01}.get(sensor))
.with_units(
{
"acc": units.METRE_PER_SECOND_SQUARED,
"gyro": units.DEGREE_PER_SECOND,
}.get(sensor)
)
.with_args(sensor=sensor, axis=axis)
for sensor in ("acc", "gyro")
for axis in ("x", "y", "z")
),
*(
htf.Measurement("{sensor}_residual_std_{axis}")
.doc("Residual standard deviation")
.in_range(0.0, {"acc": 5.0, "gyro": 0.3}.get(sensor))
.with_units(
{
"acc": units.METRE_PER_SECOND_SQUARED,
"gyro": units.DEGREE_PER_SECOND,
}.get(sensor)
)
.with_args(sensor=sensor, axis=axis)
for sensor in ("acc", "gyro")
for axis in ("x", "y", "z")
),
*(
htf.Measurement("{sensor}_residual_p2p_{axis}")
.doc("Residual peak-to-peak")
.in_range(
0.0,
{
"acc": {"x": 15.0, "y": 15.0, "z": 35.0},
"gyro": {"x": 2.0, "y": 2.0, "z": 2.0},
}[sensor][axis],
)
.with_units(
{
"acc": units.METRE_PER_SECOND_SQUARED,
"gyro": units.DEGREE_PER_SECOND,
}.get(sensor)
)
.with_args(sensor=sensor, axis=axis)
for sensor in ("acc", "gyro")
for axis in ("x", "y", "z")
),
*(
htf.Measurement("{sensor}_r2_{axis}")
.doc("Coefficient of determination R² (unitless)")
.in_range(0.5, 1.0)
.with_args(sensor=sensor, axis=axis)
for sensor in ("acc", "gyro")
for axis in ("x", "y", "z")
),
)
def compute_sensors_calibration(test: Test) -> None:
"""Perform calibration and metrics computation for both accelerometer and gyroscope."""
for sensor, data_key, calibration_key in [
("acc", "acc_data", "acc_calibration_results"),
("gyro", "gyro_data", "gyro_calibration_results"),
]:
sensor_data = test.state[data_key]
temperature = sensor_data["temperature"]
axes_data = {axis: sensor_data[f"{sensor}_{axis}"]
for axis in ["x", "y", "z"]}
test.state[calibration_key] = calibrate_sensor(
(temperature, *axes_data.values()), sensor
)
for axis, axis_data in axes_data.items():
fitted_values = test.state[calibration_key]["fitted_values"][f"{axis}_axis"]
residuals = compute_residuals(axis_data, fitted_values)
r2 = compute_r2(axis_data, fitted_values)
test.measurements[f"{sensor}_polynomial_coefficients_{axis}"] = test.state[
calibration_key]["polynomial_coefficients"][f"{axis}_axis"].tolist()
test.measurements[f"{sensor}_residual_mean_{axis}"] = abs(
residuals["mean_residual"]
)
test.measurements[f"{sensor}_residual_std_{axis}"] = residuals[
"std_residual"
]
test.measurements[f"{sensor}_residual_p2p_{axis}"] = residuals[
"p2p_residual"
]
test.measurements[f"{sensor}_r2_{axis}"] = r2
for axis, fig in zip(["x", "y", "z"],
test.state[calibration_key]["figures"]):
test.attach(
f"{sensor}_calibration_figure_{axis}",
fig.getvalue(),
"image/png")
@plug(dut=MockDutPlug)
def save_calibration(test: Test, dut: MockDutPlug) -> None:
"""Save calibration data to the DUT."""
dut.save_accelerometer_calibration(test.state["acc_calibration_results"])
dut.save_gyroscope_calibration(test.state["gyro_calibration_results"])
def main():
test = htf.Test(
connect_dut,
get_calibration_data,
compute_sensors_calibration,
save_calibration,
procedure_id="FVT1",
part_number="PCB01",
)
with TofuPilot(test):
test.execute(lambda: "00001")
if __name__ == "__main__":
main()Key Functions
Raw Data Retrieval
The script starts by retrieving raw data logged by the IMU beforehand. A method is created in an OpenHTF plug to simulate the DUT driver and retrieve raw data from its internal memory or SD card. For this example, it's a simple mock function that fetches a CSV file stored in the data folder.
import time
from pathlib import Path
from typing import Dict
from openhtf import Test
from openhtf.plugs import BasePlug
from pandas import DataFrame, read_csv
class MockDutPlug(BasePlug):
"""
A mock plug for simulating communication with a DUT.
Provides methods to connect, disconnect, and save calibration data for the DUT.
"""
def connect(self) -> None:
self.logger.info("Simulated: Connecting to DUT.")
time.sleep(1)
def disconnect(self) -> None:
self.logger.info("Simulated: Disconnecting from DUT.")
time.sleep(1)
@staticmethod
def get_imu_data(test: Test) -> Dict:
data = read_csv("data/imu_raw_data.csv", delimiter="\t")
test.attach("raw_calibration_data", data.to_csv(), "text/csv")
return {
"acc_data": {
"temperature": data["imu.temperature"],
"acc_x": data["imu.acc.x"],
"acc_y": data["imu.acc.y"],
"acc_z": data["imu.acc.z"]
- 9.80600,
},
"gyro_data": {
"temperature": data["imu.temperature"],
"gyro_x": data["imu.gyro.x"],
"gyro_y": data["imu.gyro.y"],
"gyro_z": data["imu.gyro.z"],
},
}
def save_accelerometer_calibration(
self, polynomial_coefficients: dict) -> None:
self.logger.info("Simulated: Saving IMU thermal calibration to DUT.")
time.sleep(0.5)
def save_gyroscope_calibration(
self, polynomial_coefficients: dict) -> None:
self.logger.info("Simulated: Saving IMU thermal calibration to DUT.")
time.sleep(0.5)
def tearDown(self) -> None:
self.logger.info("Simulated: Performing teardown.")
self.disconnect()Raw Data Validation
The raw measurements recorded during calibration are critical for defining the calibration parameters that will significantly impact the product's future performance. However, these measurements can be affected by testing conditions or faulty sensors. To prevent such issues, we validate the data by implementing measurements on the noise density and temperature sensitivity.
Noise Density
Sensor measurements will inevitably include noise caused by vibrations from the chamber, the support, or the sensor itself. This is not an issue, as the calibration algorithm filters out this noise. However, excessive noise could compromise calibration quality, such as when the support is poorly fixed, the chamber vibrates excessively, or a sensor is inherently too noisy. To address this, we calculate the noise density using a utility function and validate it against thresholds using OpenHTF measurements validation mechanisms.
The datasheet specifies initial noise density limits, which can later be refined using actual production data by computing the mean +/- 3 sigma values. Connecting your test scripts to TofuPilot streamlines this process, as all measurements are logged, and control charts automatically calculate the 3 sigma limits.
import numpy as np
def compute_noise_density(data: np.ndarray, sampling_rate: int = 100) -> float:
"""
Computes noise density for sensor data.
Parameters:
data (numpy.ndarray): Raw sensor data.
sampling_rate (int): Sensor sampling rate in Hz.
Returns:
float: Noise density in units/sqrt(Hz).
"""
initial_samples = data[:50]
detrended_data = initial_samples - np.mean(initial_samples)
noise_std = np.std(detrended_data)
noise_density = noise_std / np.sqrt(sampling_rate)
return noise_densityTemperature Sensitivity
If the goal of the entire process is to characterize the thermal sensitivity of sensors for accurate compensation models, estimating it beforehand is valuable to identify abnormal values. Low sensitivity may indicate that the climate chamber was not launched or that temperature variation was insufficient, while excessively high sensitivity could signal sensor defects.
We compute the temperature sensitivity across the entire thermal range and apply validations on both the maximum sensitivity measured and the sensitivity at 25°C. Initial limits are derived from the sensor datasheet and are refined over time using production data, using +/- 3 sigma values computed by TofuPilot.
import numpy as np
def compute_temp_sensitivity(
data: np.ndarray, temperatures: np.ndarray, temp_ref: float = 25
) -> dict:
"""
Computes temperature sensitivity for sensor data.
Parameters:
data (numpy.ndarray): Sensor data.
temperatures (numpy.ndarray): Corresponding temperatures for the data.
temp_ref (float): Reference temperature for sensitivity calculations (default: 25°C).
Returns:
dict: Maximum sensitivity and sensitivity at reference temperature.
"""
d_temp = np.diff(temperatures)
valid_idx = np.abs(d_temp) > 1e-5
d_data = np.diff(data)
sensitivities = d_data[valid_idx] / d_temp[valid_idx]
ref_idx = np.argmin(np.abs(temperatures - temp_ref))
ref_range = slice(max(ref_idx - 10, 0),
min(ref_idx + 10, len(sensitivities)))
sensitivity_ref = np.mean(sensitivities[ref_range])
return {
"max_sensitivity": np.max(np.abs(sensitivities)),
"sensitivity_at_ref": abs(sensitivity_ref),
}Polynomial Calibration
With raw data validated, we can proceed with the calibration process. At its core is a function that uses a 3rd-order polynomial fit to model the relationship between sensor response and temperature, generating three coefficients. These coefficients replace the need for large lookup tables and are programmed into the device, enabling real-time correction of measurements during operation.
from io import BytesIO
from typing import Dict, List, Tuple
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
matplotlib.use("Agg")
def calibrate_sensor(
data: Tuple[List[float], List[float], List[float], List[float]],
sensor: str,
polynomial_order: int = 3,
) -> Dict[str, Dict[str, np.ndarray]]:
"""
Fit a polynomial model to the sensor data against temperature.
Args:
data (tuple): A tuple containing:
- temperature data (numpy array)
- sensor data for each axis (numpy arrays for x, y, z)
polynomial_order (int): The degree of the polynomial to fit.
Returns:
dict: A dictionary containing:
- polynomial_coefficients: Coefficients of the fitted polynomial for each axis.
- fitted_values: Fitted values for each axis at the given temperature points.
- figures: Matplotlib figure objects as in-memory images for each axis.
"""
colors = {
"zinc": "#09090B",
"white": "#ffffff",
"lime": "#bef264",
"pink": "#f9a8d4",
}
temp, *sensor_data = (np.array(arr) for arr in data)
poly_coeffs: Dict[str, np.ndarray] = {}
fitted_values: Dict[str, np.ndarray] = {}
figures: List[BytesIO] = []
axis_list = ("x", "y", "z")
for i, axis_data in enumerate(sensor_data):
if sensor == "acc":
sensor_name = "Accelerometer"
unit = "m/s²"
else:
sensor_name = "Gyroscope"
unit = "°/s"
axis_name = f"{axis_list[i]}_axis"
coeffs = np.polyfit(temp, axis_data, polynomial_order)
poly_coeffs[axis_name] = coeffs
fitted = np.polyval(coeffs, temp)
fitted_values[axis_name] = fitted
residuals = axis_data - fitted
fig, axs = plt.subplots(
2, 1, figsize=(8, 10), gridspec_kw={"height_ratios": [3, 1]}
)
fig.patch.set_facecolor(colors["zinc"])
axs[0].set_facecolor(colors["zinc"])
axs[1].set_facecolor(colors["zinc"])
axs[0].plot(
temp, axis_data, ".",
color=colors["lime"], label=f"{sensor_name} data")
axs[0].plot(
temp, fitted, "-",
color=colors["pink"], label="Fitted Curve")
axs[0].set_title(
f"{sensor_name} {axis_name[0].capitalize()} axis calibration",
color=colors["white"])
axs[0].set_xlabel("Temperature (°C)", color=colors["white"])
axs[0].set_ylabel(f"{sensor_name} value ({unit})", color=colors["white"])
axs[0].tick_params(colors=colors["white"])
for spine in axs[0].spines.values():
spine.set_color(colors["white"])
axs[0].legend(
facecolor=colors["zinc"],
edgecolor=colors["white"],
labelcolor=colors["white"])
axs[1].hist(residuals, bins=30, color=colors["lime"],
edgecolor=colors["white"], alpha=0.8)
axs[1].set_title(
f"Residual distribution ({sensor_name.lower()} {axis_name[0].capitalize()} axis)",
color=colors["white"])
axs[1].set_xlabel(f"Residual value ({unit})", color=colors["white"])
axs[1].set_ylabel("Occurences", color=colors["white"])
axs[1].tick_params(colors=colors["white"])
for spine in axs[1].spines.values():
spine.set_color(colors["white"])
plt.subplots_adjust(hspace=0.3)
buffer = BytesIO()
plt.savefig(buffer, format="png")
buffer.seek(0)
figures.append(buffer)
plt.close(fig)
return {
"polynomial_coefficients": poly_coeffs,
"fitted_values": fitted_values,
"figures": figures,
}Calibration Validation
With the calibration parameters computed, the next step is to validate their quality by ensuring the sensor model accurately represents the sensor's response.
Residuals
To do this, we compute residuals — the differences between the model's predictions and actual measurements — and assess their characteristics. First, we compute the residual mean to identify biases, such as consistent overestimation or underestimation. Next, we compute the residual standard deviation to measure variability across the temperature range, revealing areas where the model may fit poorly. Finally, we compute the residual peak-to-peak values to assess the overall range of errors. These validations ensure the calibration is reliable and flag DUTs needing further review or rejection.
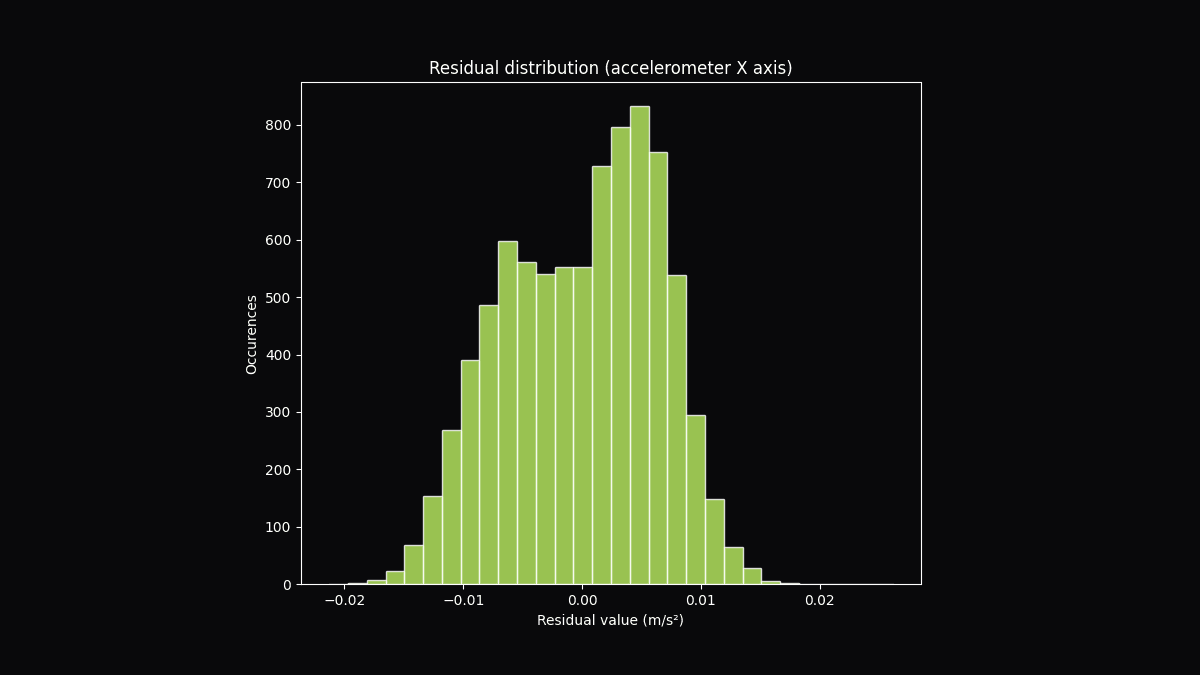
Residuals help assess the quality of the calibration.
import numpy as np
def compute_residuals(data: np.ndarray, fit_model: np.ndarray) -> dict:
"""
Computes residuals between sensor data and a fitted model.
Parameters:
data (numpy.ndarray): Sensor data.
fit_model (numpy.ndarray): Fitted model values for the same data.
Returns:
dict: Mean, standard deviation, and peak-to-peak residuals.
"""
residuals = data - fit_model
return {
"mean_residual": np.mean(residuals),
"std_residual": np.std(residuals),
"p2p_residual": np.ptp(residuals),
}Coefficient of Determination (R squared)
Residual metrics focus on local calibration accuracy, but the coefficient of determination (R squared) evaluates how well the model represents the sensor's behavior globally. A high R squared (close to 1) indicates the model explains most of the variance, while a low or negative R squared reveals poor calibration.
import numpy as np
def compute_r2(data: np.ndarray, fit_model: np.ndarray) -> float:
"""
Computes R-squared to evaluate how well a model fits the data.
Parameters:
data (numpy.ndarray): Sensor data.
fit_model (numpy.ndarray): Fitted model values for the data.
Returns:
float: R-squared value.
"""
residuals = data - fit_model
total_variation = np.sum((data - np.mean(data)) ** 2)
residual_variation = np.sum(residuals**2)
r2 = 1 - residual_variation / total_variation
return r2Database & Analytics
Sensor calibration, while complex, can be implemented quickly using tools like Python and OpenHTF. This process can be developed during the validation or development phase of a new product and deployed in production when mass manufacturing begins. The quality of a test relies not only on the performance of processing algorithms and the expertise of the team but also heavily on the choice of metrics used to validate the measurements. These metrics improve as more units are tested, allowing for more precise 3 sigma limits to be defined.
To achieve this, it is essential to have a database in place to log test results and an analytics solution from the outset. This enables tracking of tested units, identifying failure causes, and refining validation limits for all units. We developed TofuPilot specifically to address these needs.
OpenHTF Integration
Integrating TofuPilot with OpenHTF is straightforward, requiring only a single line of code. This allows you to log test results automatically, enabling real-time tracking, analytics, and the refinement of validation metrics without disrupting your existing workflow.
Run Page
After a run has completed, a dedicated page is automatically created in your secure TofuPilot workspace. This page displays the test metadata, such as the serial number, run date, and procedure reference. It also provides the list of the run phases and measurements, along with their limits, units, duration and status. Additionally, any attachments generated during the test are automatically uploaded, making them easily accessible directly from the workspace.
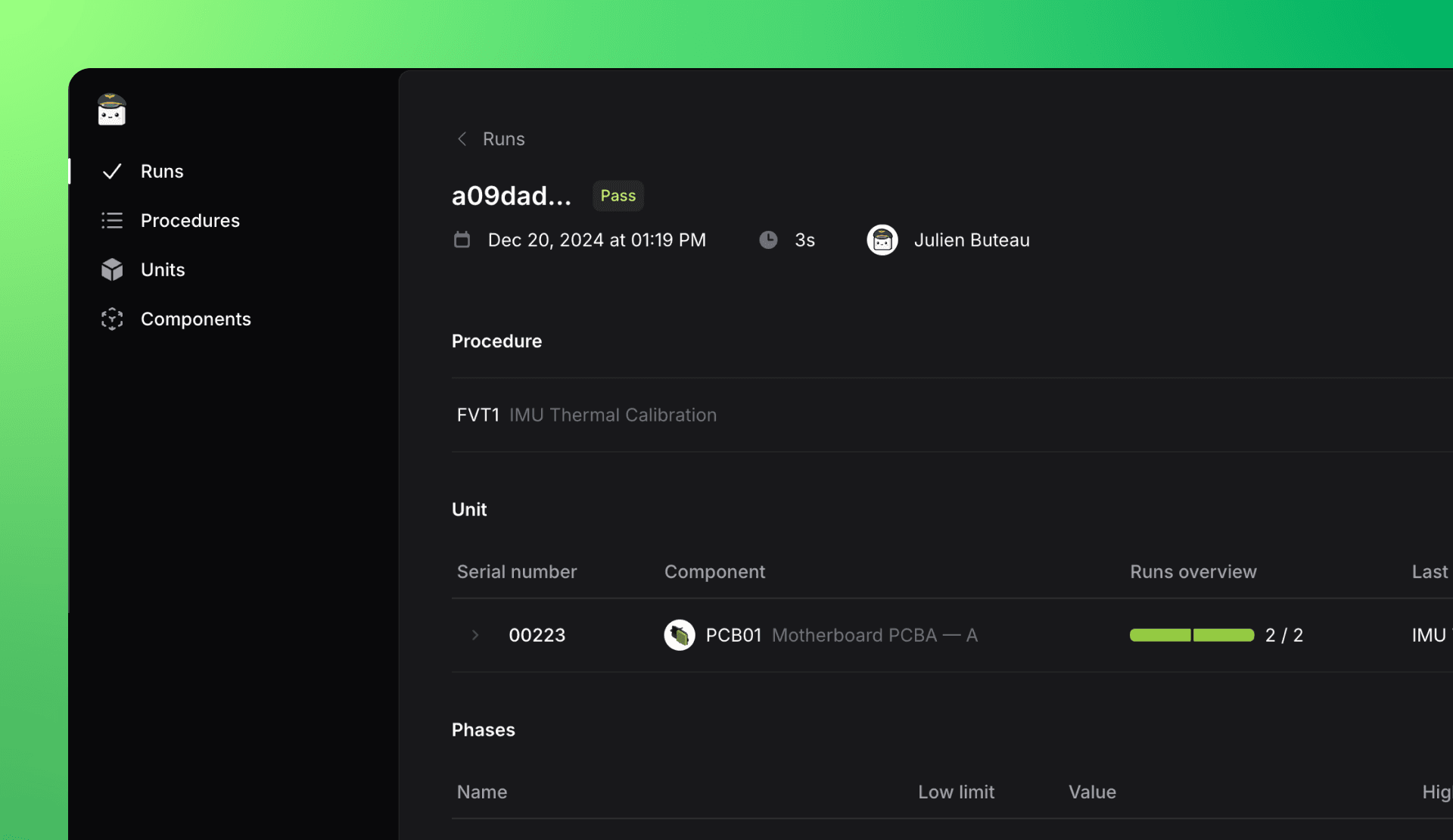
Run page displaying detailed test reports with phases and measurements.
Procedure Analytics
Analyzing the performance of a procedure across recent runs is straightforward with the procedure analytics page. Key metrics such as the run count, average test time, first pass yield, and CPK are calculated automatically. You can filter the data by date, revision, or batch to narrow down your analysis. The page also provides a detailed breakdown of performance by phase and measurement, allowing you to select a specific phase or measurement to analyze its duration, first pass yield, or CPK individually. Additionally, you can view its control chart to track recent measurements, observe trends, and determine 3 sigma values.
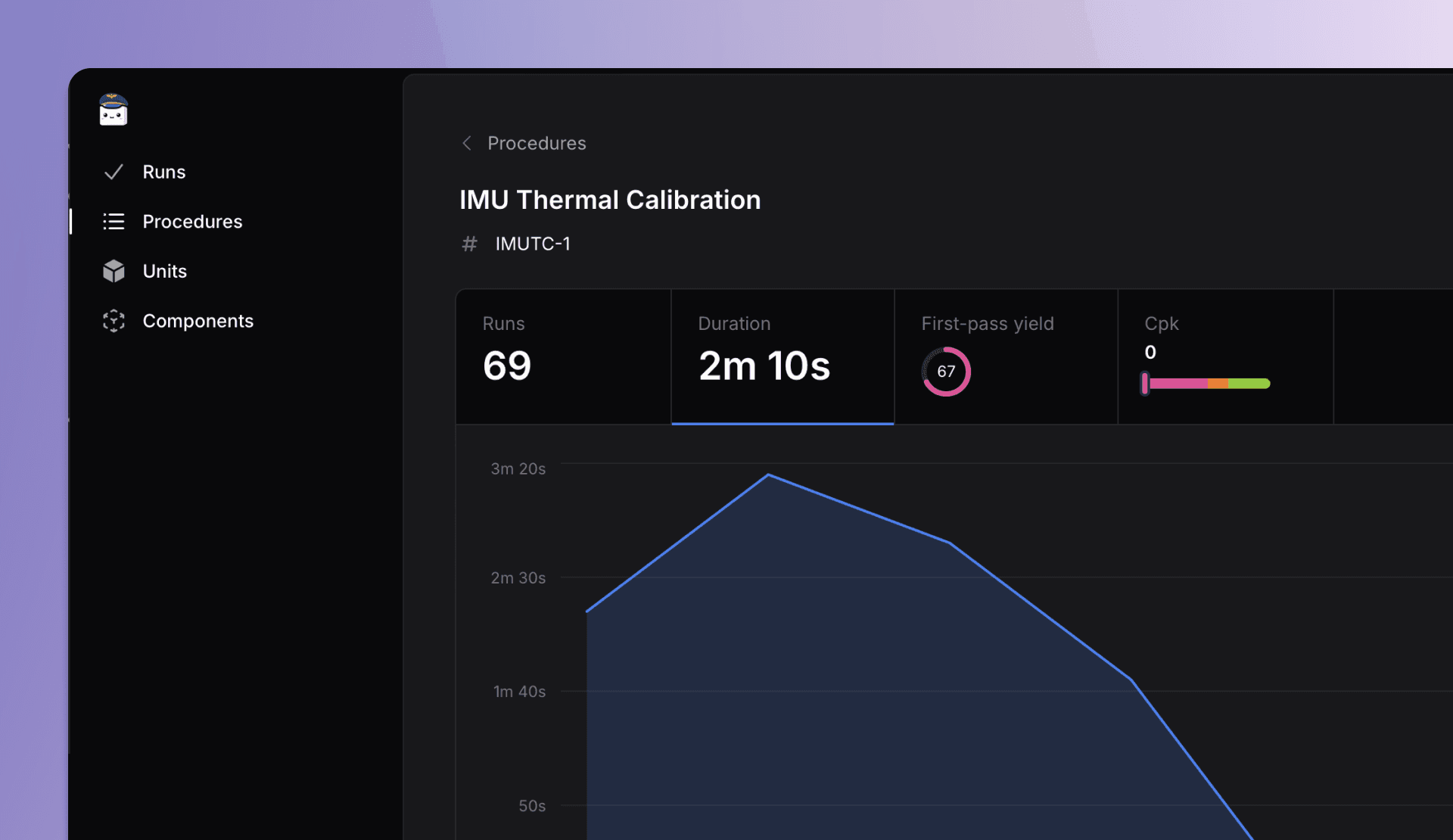
Procedure page with performance metrics, filters, and control charts.
Unit Traceability
Finally, the traceability of each tested unit is easily accessible through its dedicated page. This page provides the complete history of tests performed for the unit, any related sub-units, and a link to the page dedicated to the revision of the part.
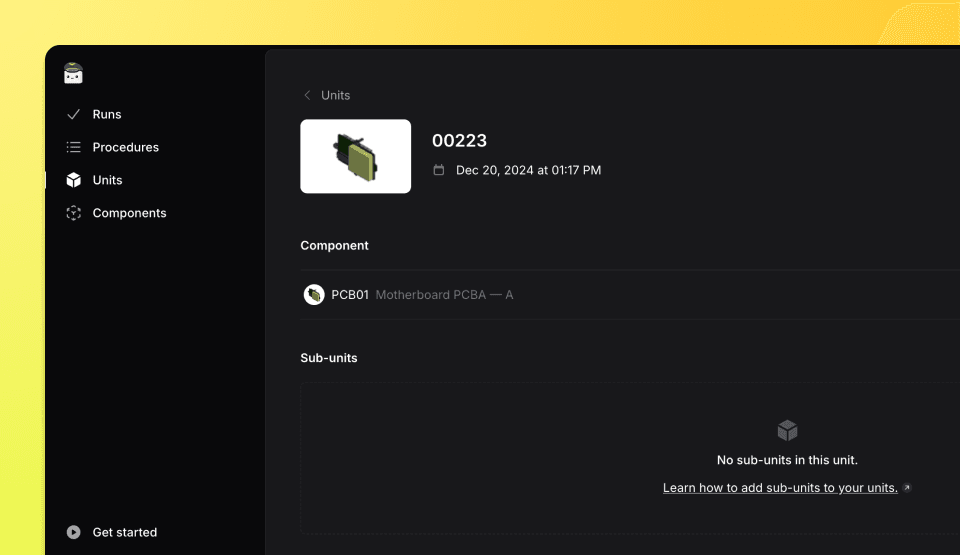
Unit page displaying the complete test history of a tested unit.